Core Tutorials
Examples
Advanced
Bound states of a finite well
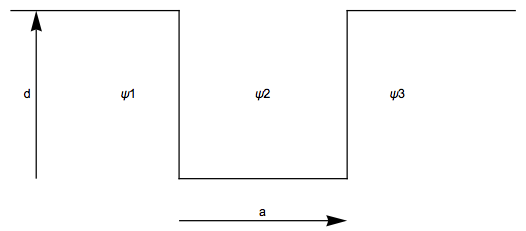
For this example lets find the wavefunction of the bound states of a quantum particle in a well using scaled units where:
First lets solve the Schrodinger equation with DSolve:
(* Region 1 and 3 *)
DSolve[psi''[x] - d^2 psi[x] == 0, psi[x], x]
(* Region 2 *)
DSolve[psi''[x] + k^2 psi[x] == 0, psi[x], x]
Two of these solutions are not physical as the wavefunction must be normalizable, and one of the integration constants can be absorbed into the unknown value for the energy. The wavefunctions, and their derivatives, in the three regions are then:
psi1 = Exp[d x]
d1 = D[psi1, x]
psi2 = a2 Cos[ k x] + a3 Sin[ k x]
d2 = D[psi2, x]
psi3 = a4 Exp[ - d x]
d3 = D[psi3, x]
In order to do the calculation numerically, we need to set the well depth (20) and width (1) in scaled units.
wellDepth = 20;
wellWidth = 1;
Next, we set up a system of equations that match the boundary conditions of both the wavefunction and its derivatives at the boundaries. Use a replacement rule (/.) to substitute the energy (en) and the well depth for the corresponding values of k and d. This linear system has 4 equations and 3 unknowns, so the Eliminate function can reduce the system to one equation:
eqs = {psi1 == psi2 /.x->0, d1 == d2 /.x->0, psi3 == psi2/.x->wellWidth, d3 == d2/.x->wellWidth}/.{d->Sqrt[-en], k->Sqrt[wellDepth+en]};
MatrixForm[eqs]
eq1 = FullSimplify[Eliminate[eqs, {a2, a3, a4}]]
Finding the roots of the equation is made easier by solving for zero and plotting. This shows that the roots are at approximately - 15 and - 4. Then use FindRoot to find the roots of this equation. Note that you will need to supply a guess to FindRoot as a starting place of the search for the root.
Plot[ en (20 + en) + 100 Sin[Sqrt[20 + en]]^2, {en, -wellDepth, 0}]
e0 = en /. FindRoot[eq1, {en, -15}]
e1 = en /. FindRoot[eq1, {en, -4}]
FindRoot can also find zeros of system of equations by supplying all of the unknowns for the system, as well as a guess for each unknown. Finding the constants for the ground state yields
roots0 = FindRoot[ eqs, { en, e0}, {a2, 1}, {a3, 1}, {a4, 1}]
Solve for the $0^th$ wave function (wf0) in each of the 3 regions and plot the result:
wf0 = ( { psi1, psi2, psi3} /. {d -> Sqrt[-en], k -> Sqrt[wellDepth + en]}) /. roots0
psi0Plot = Plot[ If[x < 0, wf0[[1]], If[x < 1, wf0[[2]], wf0[[3]]]], {x, -1, 2}]
Finding the constants for the first excited state yields
roots1 = FindRoot[ eqs, { en, e1}, {a2, 1}, {a3, 1}, {a4, 1}]
Solve for the $1^st$ wave function (wf1) in each of the 3 regions and plot the result:
wf1 = ( { psi1, psi2, psi3} /. {d -> Sqrt[-en], k -> Sqrt[wellDepth + en]}) /. roots1
psi1Plot = Plot[ If[x < 0, wf1[[1]], If[x < 1, wf1[[2]], wf1[[3]]]], {x, -1, 2}, PlotStyle -> Red]
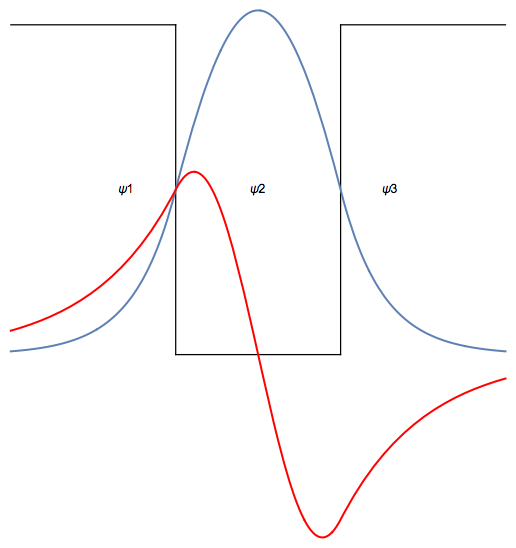
Finally put it all together with a picture of the well and the wavefunctions
wellPic = Graphics[{Line[{{0, 0}, {1, 0}}], Line[{{0, 0}, {0, 2}}],
Line[{{1, 0}, {1, 2}}], Line[{{-1, 2}, {0, 2}}],
Line[{{1, 2}, {2, 2}}], Text["\[Psi]1", {-0.3, 1}],
Text["\[Psi]2", {0.5, 1}], Text["\[Psi]3", {1.3, 1}]}];
Show[wellPic, psi0Plot, psi1Plot]